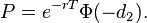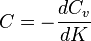Advanced formulas for binary options trading

Sponsored ads:

This page is definitely not for everybody, it is probably too much for most people.

It can be of great value if you want a deep understanding of advanced trading formulas, if that’s too “mathematical” for you can skip now to stock investment course without feeling bad.

Black–Scholes valuation

In the Black–Scholes model, the price of the option can be found by the formulas below.^[20] In fact, the Black–Scholes formula for the price of a vanilla call option (or put option) can be interpreted by decomposing a call option into an asset-or-nothing call option minus a cash-or-nothing call option, and similarly for a put – the binary options are easier to analyze, and correspond to the two terms in the Black–Scholes formula.

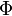In these, S is the initial stock price, K denotes the strike price, T is the time to maturity, q is the dividend rate, r is the risk-free interest rate and $\sigma$ is the volatility. $\Phi$ denotes the cumulative distribution function of the normal distribution,

Sponsored ads:

\Phi(x) = \frac{1}{\sqrt{2 \pi}} \int_{-\infty}^x e^{-\frac{1}{2} z^2} dz.

and,

d_1 = \frac{\ln\frac{S}{K} + (r-q+\sigma^{2}/2)T}{\sigma\sqrt{T}},\,d_2 = d_1-\sigma\sqrt{T}. \,

Cash-or-nothing call

This pays out one unit of cash if the spot is above the strike at maturity. Its value now is given by

C = e^{-rT}\Phi(d_2). \,

Cash-or-nothing put

This pays out one unit of cash if the spot is below the strike at maturity. Its value now is given by

P = e^{-rT}\Phi(-d_2). \,

Asset-or-nothing call

This pays out one unit of asset if the spot is above the strike at maturity. Its value now is given by

Sponsored ads:

C = Se^{-qT}\Phi(d_1). \,

Asset-or-nothing put

This pays out one unit of asset if the spot is below the strike at maturity. Its value now is given by

P = Se^{-qT}\Phi(-d_1). \,

Foreign exchange

If we denote by S the FOR/DOM exchange rate (i.e., 1 unit of foreign currency is worth S units of domestic currency) we can observe that paying out 1 unit of the domestic currency if the spot at maturity is above or below the strike is exactly like a cash-or nothing call and put respectively. Similarly, paying out 1 unit of the foreign currency if the spot at maturity is above or below the strike is exactly like an asset-or nothing call and put respectively. Hence if we now take

r_{FOR}

, the foreign interest rate,

r_{DOM}

, the domestic interest rate, and the rest as above, we get the following results.

In case of a digital call (this is a call FOR/put DOM) paying out one unit of the domestic currency we get as present value,

C = e^{-r_{DOM} T}\Phi(d_2) \,

In case of a digital put (this is a put FOR/call DOM) paying out one unit of the domestic currency we get as present value,

P = e^{-r_{DOM}T}\Phi(-d_2) \,

While in case of a digital call (this is a call FOR/put DOM) paying out one unit of the foreign currency we get as present value,

C = Se^{-r_{FOR} T}\Phi(d_1) \,

and in case of a digital put (this is a put FOR/call DOM) paying out one unit of the foreign currency we get as present value,

P = Se^{-r_{FOR}T}\Phi(-d_1) \,

Skew

In the standard Black–Scholes model, one can interpret the premium of the binary option in the risk-neutral world as the expected value = probability of being in-the-money * unit, discounted to the present value. The Black–Scholes model relies on symmetry of distribution and ignores the skewness of the distribution of the asset. Market makers adjust for such skewness by, instead of using a single standard deviation for the underlying asset $\sigma$ across all strikes, incorporating a variable one $\sigma(K)$ where volatility depends on strike price, thus incorporating the volatility skew into account. The skew matters because it affects the binary considerably more than the regular options.

A binary call option is, at long expirations, similar to a tight call spread using two vanilla options. One can model the value of a binary cash-or-nothing option, C, at strikeK, as an infinitessimally tight spread, where $C_v$ is a vanilla European call:

C = \lim_{\epsilon \to 0} \frac{C_v(K-\epsilon) - C_v(K)}{\epsilon}

Thus, the value of a binary call is the negative of the derivative of the price of a vanilla call with respect to strike price:

C = -\frac{dC_v}{dK}

When one takes volatility skew into account, $\sigma$ is a function of $K$ :

C = -\frac{dC_v(K,\sigma(K))}{dK} = -\frac{\partial C_v}{\partial K} - \frac{\partial C_v}{\partial \sigma} \frac{\partial \sigma}{\partial K}

The first term is equal to the premium of the binary option ignoring skew:

-\frac{\partial C_v}{\partial K} = -\frac{\partial (S\Phi(d_1) - Ke^{-rT}\Phi(d_2))}{\partial K} = e^{-rT}\Phi(d_2) = C_{noskew}

$\frac{\partial C_v}{\partial \sigma}$ is the Vega of the vanilla call; $\frac{\partial \sigma}{\partial K}$ is sometimes called the “skew slope” or just “skew”. Skew is typically negative, so the value of a binary call is higher when taking skew into account.